KIAS Algebraic Geometry MeetingDate: Dec. 11 - 12 , 2015 Place : 1423, KIAS |

| Program | Home > Program |
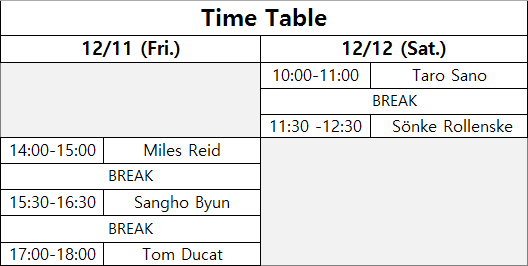
Speaker : Miles Reid (KIAS and Warwick)
Title : Diptych varieties and big skew matrixes
Abstract : This is experimental material, exploring the possibility of writing
the equations of diptych varieties as the Pfaffians of big skew matrixes, generalising
the well known extrasymmetric matrixes corresponding to Tom unprojections.
the equations of diptych varieties as the Pfaffians of big skew matrixes, generalising
the well known extrasymmetric matrixes corresponding to Tom unprojections.
Title : Stability of nets of quadrics in P^5 and associated discriminants
Abstract : Let S be a complete intersection surface defined by a net N of quadrics
in P^5. In this talk we analyze GIT stability of nets of quadrics in P^5 up to projective
equivalence and discuss some connections between a net of quadrics and the associated
discriminant sextic curve. In particular, we prove that if S is normal and the discriminant
of S is stable then N is stable. And we prove that if S has the reduced discriminant
and the discriminant is stable then N is stable. Moreover, we prove that if S has
simple singularities then the discriminant has simple singularities.
in P^5. In this talk we analyze GIT stability of nets of quadrics in P^5 up to projective
equivalence and discuss some connections between a net of quadrics and the associated
discriminant sextic curve. In particular, we prove that if S is normal and the discriminant
of S is stable then N is stable. And we prove that if S has the reduced discriminant
and the discriminant is stable then N is stable. Moreover, we prove that if S has
simple singularities then the discriminant has simple singularities.
Title : Unprojection and Mori extractions from singular curves: type A case
Abstract :We consider 3-dimensional terminal divisorial extractions from a singular
curve C in a smooth 3-fold X in the case that the general hyperplane section through
C has type A Du Val singularities. I will explain how you can construct such extractions
using serial unprojection.
curve C in a smooth 3-fold X in the case that the general hyperplane section through
C has type A Du Val singularities. I will explain how you can construct such extractions
using serial unprojection.
Title : A bound of singularities on a Q-Fano 3-fold via certain invariant of a singularity
Abstract : Namikawa proved that a Fano 3-fold with only terminal Gorenstein
singularities admits a smoothing and, as an application, he established a bound of
number of singular points on such a Fano 3-fold by using the Euler number of a
smoothed Fano 3-fold and certain invariant of a terminal singularity. In this talk,
I will talk about a generalization of this formula in the non-Gorenstein case.
singularities admits a smoothing and, as an application, he established a bound of
number of singular points on such a Fano 3-fold by using the Euler number of a
smoothed Fano 3-fold and certain invariant of a terminal singularity. In this talk,
I will talk about a generalization of this formula in the non-Gorenstein case.
Speaker : Sönke Rollenske (Marburg)
Title : Classification and moduli of stable surfaces
Abstract : The moduli space of stable surfaces is a modular compactification of
Giesecker's moduli space of canonical models of surfaces of general type. I will
give give a quick overview how much (or how little) we know about stable surfaces
and then focus on some particular examples of Gorenstein stable surfaces with
K^2 =1. This is based on joint work with Marco Franciosi and Rita Pardini.
Giesecker's moduli space of canonical models of surfaces of general type. I will
give give a quick overview how much (or how little) we know about stable surfaces
and then focus on some particular examples of Gorenstein stable surfaces with
K^2 =1. This is based on joint work with Marco Franciosi and Rita Pardini.
