Cluster Algebras and Log GW Invariants in GS program
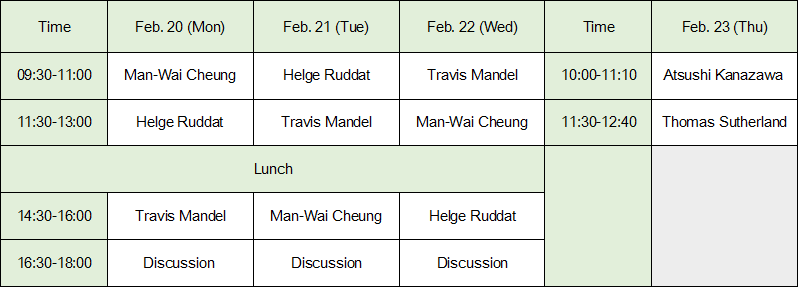
Date: February 20-22, 2017 Place: Room 8101, KIAS |
| Program | Home > Program |
File : Notes_Travis Mandel.pdf
Relation of Gross-Siebert program with cluster algebras and quiver representations (Man-Wai Cheung)
Talk 1. Introduction to toric degeneration
Talk 2. Cluster algebras and quiver representations
Talk 3. The relation and application of scattering diagram to quiver Grassmannian
Scattering diagrams theta functions and broken lines were developed by Kontsevich-Soibelman, Gross-Siebert, Gross, Siebert-Carl-Pauperla, Gross-Hacking-Keel in order to describe toric degenerations of Calabi-Yau varieties and construct mirror pairs. Later, Gross-Hacking-Keel-Kontsevich unravel the relation of those objects with cluster algebras. In the lecture series, we will first discuss the origin of scattering diagrams and theta functions from the mirror symmetry point of view. Then we will go over notions in cluster algebras. At the end, we will see how these independent concepts are linked up together.
Theta functions and log Gromov-Witten invariants (Travis Mandel)
Talk 1. Descendant log GW invariants are tropical curve counts
Talk 1. Descendant log GW invariants are tropical curve counts
Talk 2. Broken lines and theta functions
Talk 3. Theta functions and log GW invariants
Talk 3. Theta functions and log GW invariants
The motivating theme for this lecture series is to show that theta functions are given by certain log GW invariants. I will start by explaining my work with Ruddat on the correspondence between descendant log GW invariants and tropical curve counts. Then I will discuss cluster varieties and explain how to use scattering diagrams and broken lines to produce the Gross-Hacking-Keel-Kontsevich theta functions on cluster varieties. I will then sketch the proof relating these theta functions to log GW invariants. I will end by mentioning a conjecture about an analogous statement relating quantum theta functions to real GW invariants.
The link of tropical and algebraic geometry through mirror symmetry (Helge Ruddat)
Talk 1. Analyticity of Gross-Siebert families
Talk 2. Correspondences of invariants
Talk 3. Tropical lines corresponding to Lagrangian lens spaces
Tropical geometry and algebraic geometry are strongly linked by mirror symmetry. This connection is particularly evident in the Gross-Siebert program. I will introduce and elaborate on recent work of mine that fits into this larger picture. This includes work with Siebert, where we extend the Gross-Siebert degenerations to analytic families. A priori, they are defined only over the power series ring. Then I will talk about some correspondences about curve counts. I will mention my work with Mandel, where we show that log Gromov-Witten (GW) invariants are tropical curve counts in a large number of situations. After that, I will discuss my work with van Garrel and Graber showing that local GW invariants are log GW invariants in a general setup. I will end by discussing my work with Yu where we transport lines on the quintic threefold through the Gross-Siebert program and obtain Lagrangian lens spaces on the mirror family.
Thursday, Seminar talks
Atsushi Kanazawa (Kyoto University)
Title: Doran-Harder-Thompson conjecture via SYZ mirror symmetry
Abstract: I will discuss the Doran-Harder-Thompson conjecture from the view point of SYZ mirror symmetry. The conjecture claims that when a Calabi-Yau manifold X degenerates to a union of two quasi-Fano manifolds (Tyurin degeneration), a mirror Calabi-Yau manifold of X can be constructed by ”gluing” the two mirror Landau-Ginzburg models of the quasi-Fano manifolds. I will confirm the conjecture in the case of elliptic curves and certain abelian surfaces. I will use a symplectic method, which is hidden in the Gross-Siebert program.
Tom Sutherland (JGU Mainz)
Title: Scattering diagrams from stability conditions
Abstract: Stability conditions on triangulated categories allow us to define moduli spaces of objects in the category which undergo wall-crossing as the stability condition varies. We will consider certain Calabi-Yau-3 triangulated categories whose space of stability conditions has a wall-and-chamber structure which 'categorifies' mutation in a corresponding cluster algebra. Following a recent article of Bridgeland I will show how to enhance this wall-and-chamber structure to a scattering diagram which in certain cases coincides with the scattering diagram associated to the cluster algebra by Gross-Hacking-Keel-Kontsevich.
