Conference on K3 surfaces and related topicsDate: Nov.16-20, 2015 Place: Rm1503, KIAS, Seoul, Korea |

| Program | Home > Program |
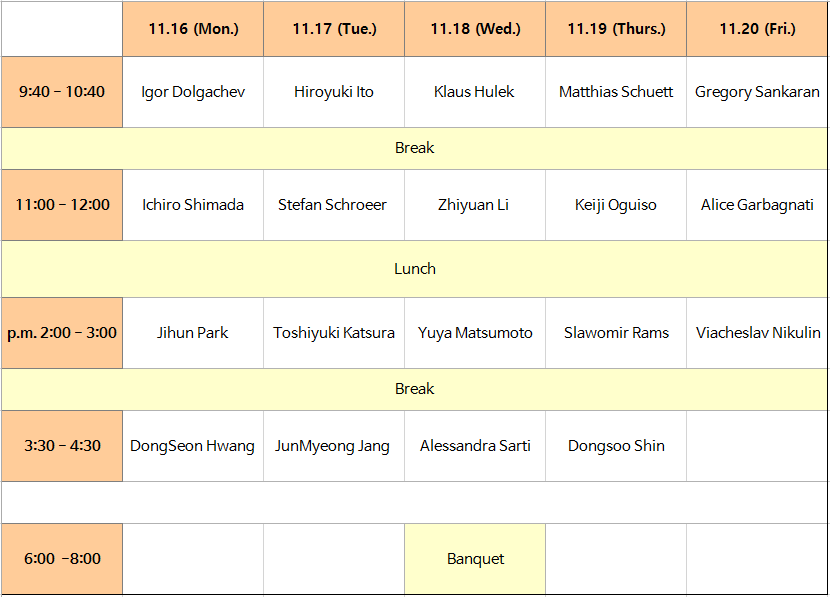
Speaker: Igor Dolgachev (University of Michigan)
Title: Lower semi-continuity of entropy in a family of surface automorphisms
Abstract: A theorem of Junyi Xie asserts that the dynamical degree of a birational automorphism of a surface varying in a smooth family is lower semicontinuous. I will give some explicit examples of families of automorphisms of Enriques and K3 surfaces when the dynamical degree goes strictly down under a specialization
Speaker: Alice Garbagnati (University of Milan)
Title: On K3 surface quotients of K3 or Abelian surfaces
Abstract: Let us denote by G a finite group. We will say that a K3 surface X is (rationally) G-covered by a surface Y if there exists a G-cover of X whose minimal model is Y. We will consider surfaces Y with trivial canonical bundle, so that Y is either an Abelian or a K3 surface. The most classical example is given by the Kummer surfaces, which are the K3 surfaces (rationally) Z/2Z-covered by an Abelian surface, but also the case of the K3 surfaces (rationally) Z/2Z-covered by a K3 surface is already known and well understood.
Speaker: DongSeon Hwang (Ajou University)
Abstract: A normal projective surface with quotient singularities is called a Q-homology projective plane if it has the same Betti numbers with the complex projective plane. In this talk, I will discuss the current state of the art on the classification of Q-homology projective planes. Gorenstein case will be treated in detail. This talk is based on the combination of joint work with JongHae Keum, Antonio Laface, Hisanori Ohashi, and Giancarlo Urzua.
Speaker: Klaus Hulek (Hannover University)
Title: Moduli of polarized Enriques surfaces
Abstract: In this talk I will discuss moduli spaces of polarized and numerically polarized Enriques surfaces. Over the complex numbers these spaces can be related to homogeneous forms and modular forms can be used to gain insight
into the geometry of these moduli spaces. As an application one obtains that there are only finitely many isomorphism classes of moduli spaces of polarized Enriques surfaces. We also show that there are moduli spaces of polarized Enriques surfaces which are of general type. This is joint work with V. Gristsenko.
Speaker: Hiroyuki Ito (Tokyo University of Science)
Title: Pseudo-derivations and wild group scheme quotient singuraities
Abstract: When one treat 2-dimestional quotient singularities in positive characteristic, most difficult and mysterious ones are wild quotient singularities which are the quotient by finite groups whose order is divisible by the characteristic.
In this talk, we consider the quotients by pseudo-derivations which are derivation-like endomorphism, and give some family of group scheme quotients as deformation families which connect Frobenius sandwich singularities and Artin-Schreier sandwich singularities under some conditions. As a result, this explains the mathematical reason for
non-tautness of many singularities of purely inseparable type.
Speaker: JunMyeong Jang (Ulsan University)
Abstract: For a K3 surface over an algebraically closed field of odd characteristic,
all the liftings over the Witt vector ring are classified by the Hodge filtration
on the second crystalline cohomology. Based on this fact, we can prove that
for a K3 surface of finite height, under a mild condition, there exists a lifting
over the Witt vector ring to which whole automorphism group can be extended.
We can also prove that a purely non-symplectic automoprhism can be lifted
over the Witt vector ring. Then, from the uniqueness of a purely non-symplectic
automorphism of high order on complex K3 surfaces, we can prove the
uniqueness of a non-symplectic automorphism of the same kind over odd
characteristic.
Speaker: Toshiyuki Katsura (Hosei University)
Title: On a classification of Enriques surfaces with finite automorphism groups
in characteristic 2
Abstract: In characteristic 0, Kondo classified Enriques surfaces with
finite automorphism groups into 7 classes. We examine, in characteristic 2, the existence of Enriques surfaces in each class. In particular, we construct classical and supersingular Enriques surfaces of type VII from a supersingular K3 surface. This work is a joint-work with S. Kondo.
Speaker: Zhiyuan Li (Stanford University)
Title: Cycle classes on moduli space of K3 surfaces
Abstract: The study of Picard groups and cohomology groups of moduli problems is started by Mumford in 1960's. In the past few decades,
there are many beautiful results known on M_g and A_g, e.g. Mumford's
conjecture. However, little is known in the case of K_g (the moduli space of
quasi-polarized K3 surfaces of genus g). According to Maulik and
Pandharipande, there is a conjectural description of the Picard group
of K_g, called Noether-Lefschetz conjecture. In this lecture, I will talk
about the recent proof of this conjecture and its generalizations.
I will also mention the relation of NL-divisors and tautological
classes on K_g. This is a joint work with Beregeron, Millson and Moeglin.
Speaker: Yuya Matsumoto (Tokyo University)
Title: Good reduction of K3 surfaces
Abstract: An abelian variety over a discrete valuation field has good reduction if and only if its l-adic cohomology group (equivalently its l-adic Tate module) is an unramified Galois representation: this is proved by Serre-Tate, and is also called the Neron-Ogg-Shafarevich criterion. We prove a similar good reduction criterion for K3 surfaces under some
conditions. To show this, we first use MMP techniques to prove good reduction over some finite Galois field extensions, and then show that we can (after some modifications) take quotients by the Galois group.
This is a joint work with Christian Liedtke.
Speaker: Keiji Oguiso (U. of Tokyo)
Title: Primitive automorphisms of positive entropy of projective hyperkaehler 4-folds and Calabi-Yau 4-folds
Abstract: We shall show one way to construct projective hyperkaehler 4-folds and Calabi-Yau 4-folds with primitive biholomorphic automorphisms of positive entropy,
starting from generic Enriques surface automorphisms. These are the
first examples in dimension greater than or equal to four, except perhaps
complex tori. Primitive automorphisms are the automorphisms which do not
preserve any non-trivial fibrations (in birtaionl sense) so that in some
sense the most basic ones of manifolds of a given dimension.
Speaker: Slawomir Rams (Jagiellonian University Cracow/Poland)
Title: Counting lines on some low-degree surfaces
Abstract: It has been shown by Prof. Schuett and myself that a line on a smooth projective quartic over a field of characteristic neq 2,3 can be met by at most 20 lines.
The proof heavily depends on the modern theory of elliptic fibrations. Thus it cannot be applied to higher-degree surfaces. In my talk I will give entirely different proof
of the above result and apply it to obtain certain results concerning configurations of lines on quintic surfaces. If time permits I will also discuss a bound on the number
of lines on smooth quartic surfaces over fields of characteristic 2 (the only characteristic where the maximal number is unknown until now).
It is joint work with prof. M. Schuett (LUH Hannover).
Speaker: Gregory Sankaran (University of Bath)
Title: Degenerating Hilbert schemes of K3 surfaces
Abstract: Degenerating families of K3 surfaces were studied by Kulikov and by Pinkham and Persson in the 1970s. The corresponding questions for other hyperkaehler manifolds are mostly still open, although Nagai considered the degeneration of length 2 Hilbert scheme corresponding to a type II degeneration of K3 surfaces. Using Nagai's approach as a starting point, we begin the study of degenerations of Hilbert schemes belonging to type III degenerations of K3 surfaces.
Speaker: Alessandra Sarti (Poitiers University)
Title: Complex ball quotients and moduli spaces of some irreducible holomorphic symplectic fourfolds
Abstract: In a well known paper Dolgachev and Kondo describe moduli spaces of K3 surfaces with non-symplectic automorphism of odd prime order as complex ball quotients.
In the talk I will generalize this construction to moduli spaces of some irreducible holomorphic symplectic
fourfolds with non-symplectic automorphism of odd prime order. I will use recent results by Amerik-Verbistky
on the Kähler cone of irreducible holomorphic symplectic manifolds and techniques developed by Joumaah. This is a joint work in progress with S. Boissière and C. Camere
Speaker: Matthias Schuett (Hannover University)
Title: Moduli of Gorenstein Q-homology fake projective planes
Abstract: Inspired by fake projective panes, this talk concerns normal projective surfaces whose Q-homology equals that of IP^2. I shall concentrate on the case of numerically trivial canonical bundle which is closely related to Enriques surfaces as investigated by Hwang-Keum-Ohashi. In the complex case, I will give a complete classification of their moduli which turn out to be rational, 1-dimensional and defined over Q. Time permitting, I will also discuss the subtleties in positive characteristic.
Speaker: Stefan Schroeer (Duesseldorf University)
Title: Wild quotient singularities
Abstract: We introduce and analyse a class of wild quotient singularities in arbitrary characteristics and dimensions, which generalizes the wild quotient surface singularities in characteristic two of Artin.
This is joint research with Dino Lorenzini.
Speaker: Ichiro Shimada (Hiroshima University)
Title: Automorphisms of supersingular K3 surfaces and Salem polynomials
Abstract: We present a method to generate many automorphisms of a supersingular K3 surface in odd characteristic. As an application, we show that, if p is an odd prime less than or equal to 7919, then every supersingular K3 surface in characteristic p has an automorphism whose characteristic poly- nomial on the N’eron?Severi lattice is a Salem polynomial of degree 22.
Speaker: Dongsoo Shin (Chungnam National University)
Speaker: Viacheslav Nikulin (University of Liverpool)
Title: Classification of degenerations of Kahlerian K3 surfaces with finite symplectic automorphism groups
Abstract: We classify degenerations of codimension one of Kahlerian K3 surfaces with finite symplectic automorphism groups. By classification we understand an enumeration of connected components of moduli spaces of the degenerations.
See our preprints arXiv:1403.6061 and 1504.00326 for some details.
Speaker: Jihun Park (IBS-CGP / Postech)
Title: Cylinders on rational surfaces
Abstract: A cylinder in a projective normal surface is a Zariski open subset isomorphic to a $mathbb{A}^1$-bundle
over a smooth affine curve. It is closely related to unipotent actions on affine cones. In this talk, we explore rational surfaces to find effective ample $mathbb{R}$-divisors such that the complements of their supports are cylinders.
