Program

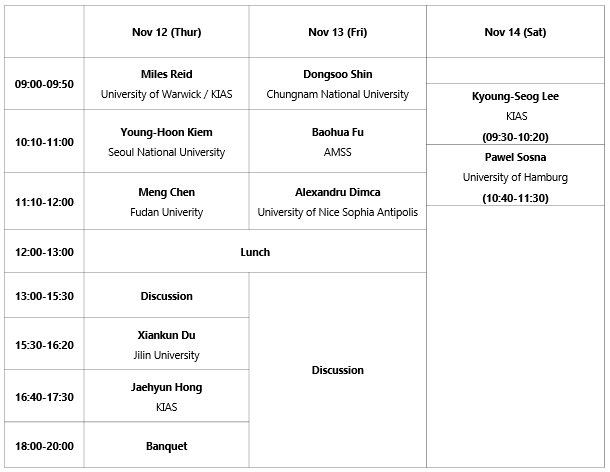
Title and Abstract of Talks

- November 12 -

Miles Reid
Title: The Oort-Tate cyclic group scheme of order p and Godeaux surfaces
Abstract:  This is joint work in progress with KIM Soonyoung, arising from her Sogang University PhD thesis, based on a problem posed by Yongnam LEE.
In characteristic p, the cyclic group ZZ/p is replaced by three different group schemes of order p. These are
  (a)  FF_p^+ defined by x^p = x with the multiplication rule (x1,x2) -> x1+x2;
  (b)  al_p defined by x^p = 0 with the multiplication rule (x1,x2) -> x1+x2;
  (c)  mu_p defined by x^p = 1 with the multiplication rule (x1,x2) -> x1*x2.
We can also write the last case (c) as y^p = 0 with the multiplication rule
(y1,y2) -> y1 + y2 + y1*y2, isomorphic to mu_p by y = 1+x.
The construction of Oort and Tate puts these three together as a single cyclic group scheme Cp defined over the line pair U : (st = 0). Over this base, it is given by
  x^p - s*x - t = 0
and has the multiplication rule (x1,x2) -> x1 + x2 + t*x1*x2. Where (s,t) = (0,0)
this gives (b). Where s is invertible it gives a form of (a), and where t is invertible it gives a form of (c).
A basic principle is that one should expect to see the Oort-Tate group scheme Cp in characteristic p wherever the cyclic group ZZ/p occurs in characteristic zero; for example as a covering group of varieties (or a fundamental group).
The Oort-Tate group scheme Cp acts on its regular representation and different tensor powers of it. This provides a natural framework to study Godeaux surfaces in characteristic 5 with Pic^tau of order 5, and Campedelli surfaces in characteristic 7 with Pic^tau of order 7, together with Calabi-Yau 3-folds extending these.
 
Young-Hoon Kiem
Title: Critical virtual manifolds and perverse sheaves
Abstract: Critical virtual manifolds are analytic spaces which are locally the critical loci of holomorphic functions on complex manifolds. In this talk, I will talk about symmetric semi-perfect obstruction theory, Donaldson-Thomas type invariant, Behrend function, perverse sheaves and mixed Hodge modules of vanishing cycles as well as their gluing, on critical virtual manifolds. Main examples are moduli spaces of stable sheaves on Calabi-Yau 3-folds and there is a direct application to the categorification problem for Donaldson-Thomas invariants. This talk is based on a joint work with Jun Li.
  
Meng Chen
Title: Characterization of the 4-canonical birationality of algebraic 3-folds whose geometric genus is 4
Abstract: For nonsingular projective 3-folds X (of general type) whose geometric genus $p_g$ is greater than 4, the birationality of the fourth canonical map $Phi_{4,X}$ was characterized by D.-Q. Zhang and the first author in 2008. Here we characterize the birationality of $Phi_{4,X}$ for those with $p_g(X)=4$. This is my joint work with Qi Zhang.
  
Xiankun Du
Title: Derivations and multidegrees for automorphisms of polynomial rings
Abstract: In this talk we first give an equivalent condition for a set of pairwise commuting derivations to be a commutative basis of $Der_k k[X]$. Then we present a criteria to determine whether a monomial derivation of the polynomial ring in three variables has Darboux polynomials or not. The kernel of a higher derivation of the polynomial ring will be proved to be generated by a set of closed polynomials. Finally, multidegrees with special forms of tame automorphisms of the polynomial ring in three variables will be discussed. This is joint work with Jiantao Li and Yang Tao.

Jaehyun Hong
Title: Cycle spaces of flag domains and standard embeddings between flag varieties
Abstract: Let $Z$ be a flag variety. A real form of the automorphism group of $Z$ acts on $Z$ and has only finitely many orbits.  Open orbits are called flag domains. It is also known that there is a unique closed orbit. The closed orbit sometimes has an interpretation as the Shilov boundary of a flag domain.  Consider a pair $(Z,Z')$ of flag varieties of subdiagram type and the action of real forms of their automorphism groups. Let $f$ be a holomorphic  embedding from a connected  open subset of $Z$ into $Z'$ which sends an open piece of the closed orbit in $Z$ into the closed orbit in $Z'$. We will explain how one can use cycle spaces of flag domains to get  an extension of $f$ to a standard embedding of $Z$ into $Z'$.  This is joint work in progress  with S.-C. Ng. 

- November 13 -

Dongsoo Shin
Title: Identifying Milnor fibers of quotient surface singularities via the minimal model program
Abstract: I provide an explicit algorithm for identifying a Milnor fiber of a smoothing of a quotient surface singularity as a symplectic filling of the singularity, that is, as a complement of the so-called compactifying divisor lying in a rational symplectic 4-manifold. For this I apply some techniques from the minimal model program for 3-folds such as divisorial contractions and flips. This is a joint work with Heesang Park, Jongil Park, and Giancarlo Urz'ua.

Baohua Fu
Title: Minimal rational curves on wonderful group compactifications
Abstract: Consider a simple algebraic group G of adjoint type, and its wonderful compactification X. We show that X admits a unique family of minimal rational curves, and we explicitly describe the subfamily consisting of curves through a general point. As an application, we show that X has the target rigidity property when G is not of type A_1 or C. This is a joint work with Michel Brion.

Alexandru Dimca
Title: Free curves and free surfaces, and their nearly free analogues
Abstract: In this talk we recall the definition of a free projective hypersurface and discuss some geometric properties of free curves and surfaces. This will lead us naturally to the definition of nearly free hypersurfaces.

- November 14 -

Kyoung-Seog Lee
Title: On the Fano visitor problem for holomorphic symplectic varieties
Abstract: Holomorphic symplectic varieties form an attractive and important class of varieties and derived categories play an important role in their study. In this talk, I will review constructions of some families of holomorphic symplectic varieties, Fano visitor problem and its recent progress. Then I will discuss Fano visitor problem for holomorphic symplectic varieties. This is a joint work in progress with Young-Hoon Kiem.

Pawel Sosna
Title: Some properties of dynamical degrees
Abstract: Dynamical degrees are numbers associated with a birational self-map of a smooth complex projective variety. Considering all birational maps at once, gives the dynamical spectrum of a variety, which is a birational invariant. It is an interesting question whether this spectrum could be useful in determining the rationality of, for example, cubic hypersurfaces. In the talk I will discuss some properties of these numbers and present some computations on cubic fourfolds. This is joint work with Chr. Böhning and H.-Chr. Graf von Bothmer.