Invariants in Low-dimensional Topology
Date: May 10-12, 2017 Place: Room 8101, KIAS |
| Program | Home > Program |
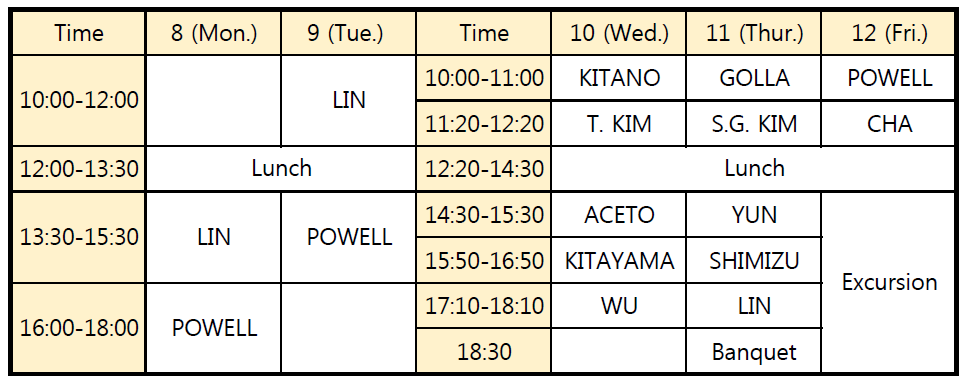
Lecture series
Speaker: Francesco Lin (IAS, Princeton University)
Workshop
Speaker : Paolo Aceto (Alfred Renyi Institute)
Title: Rational homology cobordisms of plumbed manifolds and arborescent link concordance
Abstract: We investigate rational homology cobordisms of 3-manifolds with non-zero first Betti number. This is motivated by the natural generalization of the slice-ribbon conjecture to multicomponent links.
In particular we consider the problem of which rational homology S^1xS^2's bound rational homology S^1xD^3's. We give a simple procedure to construct rational homology cobordisms between plumbed 3-manifold. We introduce a family F of plumbed 3-manifolds with b_1=1. By adapting an obstruction based on Donaldson's diagonalization theorem we characterize all manifolds in F that bound rational homology S^1xD^3's. For all these manifolds a rational homology cobordism to S^1xS^2 can be constructed via our procedure. The family F is large enough to include all Seifert fibered spaces over the 2-sphere with vanishing Euler invariant.
We also describe applications to arborescent link concordance.
Speaker : Jae Choon Cha (POSTECH)
Title : Whitney towers in a rational homology ball
Abstract : I will discuss a complete classification of links in the 3-space modulo Whitney towers in a rational homology 4-ball. This gives a new geometric interpretation of the Milnor invariants, and an alternative viewpoint to the higher order Arf invariant conjecture.
Speaker : Marco Golla (Uppsala University)
Speaker : Se-Goo Kim (Kyung Hee University)
Title : Secondary Upsilon invariants of knots
Abstract : The knot invariant Upsilon, defined by Ozsváth, Stipsicz, and Szabó, induces a homomorphism from the smooth knot concordance group to the group of piecewise linear functions on the interval [0, 2]. Here we define a set of related secondary invariants, each of which assigns to a knot a piecewise linear function on [0, 2]. These secondary invariants provide bounds on the genus and concordance genus of knots. Examples of knots for which Upsilon vanishes but which are detected by these secondary invariants are presented. This is a joint work with Charles Livingston.
Speaker : Taehee Kim (Konkuk University)
Title : Structure of the grope filtration of the knot concordance group
Abstract : A grope in the 4-ball bounded by a knot in the 3-sphere is a certain 2-complex which can be considered as an approximation of a slice disk. Cochran, Orr, and Teichner defined a filtration of the knot concordance group using gropes. In this talk, I will give a new infinite rank subgroup for each of the successive quotients of the filtration. A key ingredient is L2-signature defects associated to amenable groups.
Speaker : Teruaki Kitano (Soka Universtiy)
Title : A polynomial invariant of a homology 3-sphere defined by Reidemeister torsion
Abstract : In the end of 1980s Dennis Johnson studied Reidemeister torsion for a homology 3-sphere
from the view point of Casson invariant, as follows.
Let M be a homology 3-sphere with a fixed Heegaard splitting. Johnson gave volume forms on the spaces of conjugacy classes of SU(2)-irreducible representations for the closed surface and handle bodies. Under some assumption, he considered a weight for each conjugacy class and proved this weight is equal to Reidemeister torsion of M for the corresponding irreducible representation composed with the adjoint representation.
Further he proposed to study polynomials whose zeros are the values of Reidemeister torsion of M for several settings.
In this talk, for SL(2;C)-representation, we would like to explain Johnson theory and show some formulas, examples, and properties, for Brieskorn homology spheres and surgeried manifolds along the figure-eight knot. Some of them concern a joint work with Anh Tran.
Speaker : Takahiro Kitayama (Tokyo University)
Title : Representation varieties detect splittings of 3-manifolds
Abstract : Culler and Shalen established a method to construct nontrivial actions of a group on trees from ideal points of its SL_2-character variety. The method, in particular, gives essential surfaces in a 3-manifold corresponding to such actions of its fundamental group. Essential surfaces in some 3-manifold are known to be not detected in the classical SL_2-theory. We show that every essential surface in a 3-manifold is given by an ideal point of the SL_n-character variety for some n. The talk is partially based on joint works with Stefan Friedl and Matthias Nagel, and also with Takashi Hara.
Speaker : Francesco Lin (IAS, Princeton University)
Title : Bar Natan's deformation of Khovanov homology and involutive monopole
Floer homology
Abstract : We study the conjugation involution in Seiberg-Witten theory in the context of the Ozsvath-Szabo and Bloom's spectral sequence for the branched double cover of a link L in S^3. We show that there exists a spectral sequence of F[Q]/Q^2-modules (where Q has degree −1) which converges to an involutive version of the monopole Floer homology of the branched double cover, and whose E^2-page is a version of Bar Natan's deformation of Khovanov homology in characteristic two of the mirror of L. We conjecture that an analogous result holds in the setting of Pin(2)-monopole Floer homology.
Speaker : Mark Powell (UQAM)
Title : Stable diffeomorphism of 4-manifolds.
Abstract : Two smooth compact 4-manifolds are said to stably diffeomorphic if one can connect sum either or both with copies of S^2 x S^2 in such a way that they become diffeomorphic. The classification of 4-manifolds up to this relation is in some cases a tractable question, especially when compared with the unstable situation. The fundamental group governs the complexity of the question to a large extent. I will discuss joint work with Daniel Kasprowski and Peter Teichner, in which we provide algebraic invariants that for many fundamental groups determine whether or not two 4-manifolds are stably diffeomorphic. We also obtain results on the
corresponding stable equivalence relation where S^2 x S^2 is replaced by the complex projective plane.
Speaker : Tatsuro Shimizu (RIMS, Kyoto University)
Title : On the Bott-Cattaneo's Chern-Simons perturbation theory
Abstract : Chern-Simons perturbation theory was established by Kontsevich, Axelrod and Singer. There are some invariants inspired by Chern-Simons perturbation theory. In this talk, I revisit Bott-Cattaneo's Chern--Simons perturbation theory. Their theory gives an invariant of a 3-manifold with a flat connection of the trivial $G$-bundle over the 3-manifold, where $G$ is a semi-simple Lie group. I give a modified construction of Bott-Cattaneo's Chern-Simons perturbation theory, and show a few examples of this invariant.
Speaker : Zhongtao Wu (CUHK)
Title : 3-manifold invariants and Dehn surgery
Abstract : The cosmetic surgery conjecture says that there is no pair of Dehn surgeries on a non-trivial knot that yield homeomorphic 3-manifolds preserving orientation. We will introduce some recent progress on this conjecture and discuss several 3-manifold invariants that are relevant to this problem. Part of this talk is based on joint work with Yi Ni and joint work with Kazuhiro Ichihara.
Speaker : Ki-Heon Yun (Sungshin University)
Title : On dissolving knot surgery 4-manifolds under a CP^2-connected sum
Abstract : In this talk we show that all knot surgery 4-manifolds E(n)_K are mutually diffeomorphic after a connected sum with CP^2. Hence, by combining a known fact that every simply connected elliptic surface is almost completely decomposable, we conclude that every knot surgery 4-manifold E(n)_K is also almost completely decomposable.
It is a joint work with Hakho Choi and Jongil Park.
