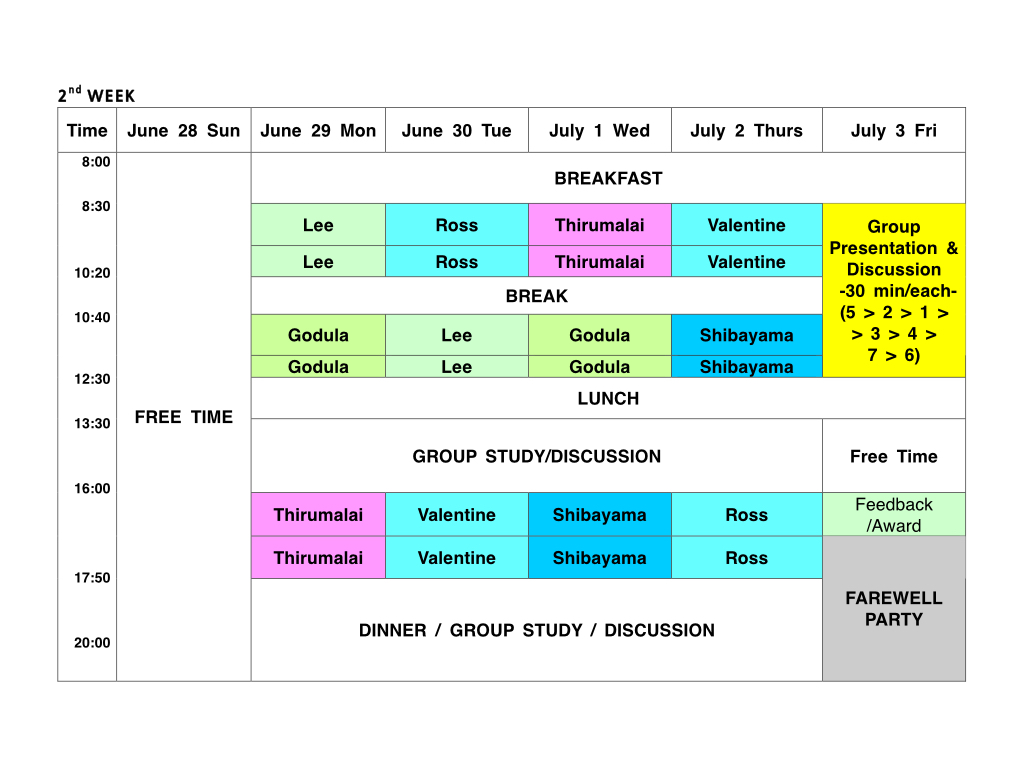
| Program | Home > Program |

List of Lecturers
M.C. Choi (KAIST) - Structures and interactions of microtubules and microtubule-associated-molecules
Lecture slide 1
Lecture slide 2
Kamil Godula (UCSD)
1) Polysaccharides - structural motifs that shape life
This first of my two lectures will survey how various molecular architectures of polysaccharides are utilized in Nature to provide structural support for living organisms.
2) Glycoproteins - breaking the sugar code
The second lecture will describe how three-dimensional presentation of carbohydrates on polypeptide scaffolds in glycoproteins encodes biological information and how synthetic glycomaterials can be used to decipher and exploit this information.
Lecture Slide 1 (Polysaccharides)
Video 1
Lecture Slide 2 (Glycoproteins)
Video 2
Kurt Kremer (MPI, Mainz) - Multiscale studies of macromolecular systems: concepts and applications
Lecture Slide 1
Lecture Slide 2
Video 1 Video 2
Jooyoung Lee (KIAS) - Protein Structure Prediction and Global Optimization
Lecture Slide 1.
Lecture Slide 2.
Video 1 Video 2
Seok-Cheol Hong (Korea Univ) - DNA mechanics and structural diversity of DNA
Lecture Slide 1
Lecture Slide 2
Lecture Slide 3
Lecture Slide 4
Video 1 Video 2
Fyl Pincus (UCSB) -Basic concept in polymer physics
Video 1 Video 2
*Some problems to master the basic polymer concepts (Problem Set)
Jennifer Ross (Univ. Mass)
Lecture Note 1
Supplement 1
Supplement 2
Supplement 3
Lecture Note 2
Video 1 Video 2
Omar Saleh (UCSB) - 1) Biopolymers in tension 2) Electrostatics of flexible biopolymers
Lecture 1
Lecture 2
Problem Set
Video 1 Video 2
Helmut Schiessel (Univ. Leiden) - Chromatin: a multi-scale jigsaw puzzle in biological physics
Slide 1
Slide 2
Slide 3
Slide 4
Problem set > Solutions
Possible group projectsVideo 1 Video 2
Ben Schuler (Univ. Zurich) - Single-molecule spectroscopy of unfolded and intrinsically disordered proteins
Lecture
Tutorial article
Video 1 Video 2
Mitsuhiro Shibayama (Univ. Tokyo)
- Neutron and Rheology (Lecture outline)
1. Structural Analyses of Polymers by Small Angle Neutron Scattering
2. Contrast Variation SANS -The basics and applications
3. Rheo-SANS Studies on Structure Evolution in Polymer-particle Aqueous Solutions.
Slide 1
Slide 2
Slide 3
Homework
Video 1 Video 2
Dave Thirumalai (Univ. Maryland)
Slide 1
Slide 2
Video 1 Video 2
Megan Valentine (UCSB) - Biopolymer network mechanics
The first 2-hour lecture will be on microrheology, with a strong emphasis on biopolymers. The second 2-hour lecture will be on cytoskeletal mechanics. Both will include lots of detail on instrumentation and *how* such experiments are performed.
Lecture slide 1
Microrheology (Gardel, Valentine, Weitz)
Lecture Slide 2
Video 1 Video 2
Each group is anticipated to prepare 30 min presentation (+discussion) for the last day of the Summer School.
1. What would be the most stable configuration of a 2-dimensional polymer, whose contour is continuously charged, with its two ends being fixed in space? (When the two ends are fixed at the same spot, the answer should be a circle. But, when they are not in the same spot, it is not clear what it should be. The answer may not be a part of circle.... Maybe, Helmut Schiessel's lecture on Euler-Lagrange equation can give you an idea, but Helmut says there seems to be little hope).
2. Stretching hair.
3. Refer to this reference. Consider chains of such decorated polymers. Derive force- extension curve. What are the properties of brushes made of these? What happens in an external electric field? This can lead to lots of thought with open questions. Many interesting limits.
4. Persistence length (lp) of ssDNA is ~ 1 nm, but lp of dsDNA is ~ 50 nm. Why?
* Consider a rotational isomer model of a polymer with fixed polar angle θ but freely rotating dihedral angle. For a single chain, calculate the persistence length. (This is a classical easily solved problem.) Take two parallel identical chains with weak springs attaching nodes (looks like a ladder). The springs will limit the randomness of the dihedral angle and should significantly stiffen the duplex, n’est ce pas? This may be doable.
* A little bit more formal approach could be possible. (see here)
5. Polymer looping dynamics is one of the most elementary processes often discussed in polymer sciences and biophysics. The looping time can be addressed in various conditions, for example, as a function of loop size, chain stiffness, and the extent of volume exclusion interaction. Also, consider many different situations of end-to-end, end-to-interior, or interior-to-interior looping.
6. What is the persistence length of polyproline ? (Polypeptide is quite flexible, whose persistence length is only a few angstrom, but polypeptide made of prolines would be different from other amino acids). You can do literature search and find out how people are measuraing and what number people are getting for the persistence length of polyproline.
7. Similar project to Question 6.... Discuss the persistence length of microtubules. What is it? and how is it measured?
8. This project may easily be done by those who know how to do computer simulations of polymers. Calculate the size (radius of gyration) of flexible polymer by increasing N (number of monomers) in a good solvent condition, and obtain the scaling exponent nu. What is the minimal size of the polymer chain (N > N*) to get nu ~ 0.588 ? and how does N* vary with the solvent condition (or the strength of 2nd virial coefficient)? How does the randomness in monomer-monomer interaction strength affect the conclusion? ...
Some interesting polymer-related articles to read.
1. Entropic Elasticity of lambda-Phage DNA
2. Stretching DNA (Marko & Siggia) Macromolecules 1995, 28:8759
3. Excluded Volume Effects and Stretched Polymer Chains, P. Pincus Macromolecules (1976)
4. Two Landmarks in Polymer Physics: The Edwards Model and de Gennes Observation (D. Thirumalai)
5. Size of a Polymer Molecule in Solution, (Edwards & Singh) J. Chem. Soc., Faraday Trans. 2, 1979,75, 1001-1019
6. Rapid Microtubule Self-Assembly Kinetics. Odde and coworkers. Cell (2011)
7. Size distribution of protein polymers, F. Oosawa, J. Theor. Biol. (1970)
8. Optical Measurements of Frequency-Dependent Linear Viscoelastic Moduli of Complex Fluids, Mason & Weitz (1995) Phys. Rev. Lett.
9. Statistics of macromolecular solutions trapped in small pore (1997) Daoud and de Gennes
10. Polyelectrolytes (F. Oosawa)
11. The statistical mechanics of polymers with excluded volume, S. F. Edwards, (1965) Proc. Phys. Soc. vol. 85 613
Copyright 2012(c) Korea Institute for advanced Study(KIAS). All rights reserved. 85 Hoegiro, Dongdaemun-gu, Seoul 02455, Republic of Korea [Admin]